给定一组样本,{1,5},{2,7},{3,9},{4,11},{5,13},根据样本预测一元线性方程y=wx+b中的w值和b值,可以用数学的最小二乘法求解,这里使用批量梯度下降法求解。
主要思想:根据y=wx+b计算出来的y值和实际y值是有误差的,根据这个误差去更新w和b的值(具体计算公式需要用到偏导数,程序中的变量“xxSum”体现了“批量”),更新速度快慢取决于学习率的大小,当w和b的值几乎不再更新时,意味计算出来的y值和实际y值的误差已经很小,这时候停止迭代,求解完成。
#include <iostream>
using namespace std;
void LinearRegression(float x[], float y[], int n, float& w, float& b)
{
float yOut;
float residual;
float deltaB = 0.0;
float deltaBSum = 0.0;
float deltaW = 0.0;
float deltaWSum = 0.0;
float learningRate = 0.01;
for (int i = 0; i < n; i++)
{
yOut = w * x[i] + b;
residual = -(yOut - y[i]);
deltaB = 1 * residual * learningRate;
deltaBSum = deltaBSum + deltaB;
deltaW = x[i] * residual * learningRate;
deltaWSum = deltaWSum + deltaW;
}
deltaB = deltaBSum / n;
deltaW = deltaWSum / n;
b = b + deltaB;
w = w + deltaW;
}
int main()
{
clock_t t1 = clock();
float x[] = { 1, 2, 3, 4, 5 }; //样本x值
float y[] = { 5, 7, 9, 11, 13 }; //样本y值
int n = 5;
float w = 1.0; //随机初始权重
float b = 1.0; //随机初始偏移
for (int i = 0; i < 1000000; i++)
{
float preW = w;
float preB = b;
LinearRegression(x, y, n, w, b);
if (fabs(w - preW) < 0.000001 && fabs(b - preB) < 0.000001)
break;
}
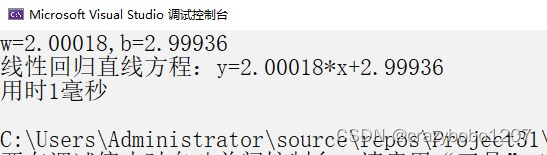
cout << "w=" << w << "," << "b=" << b << endl;
cout << "线性回归直线方程:y=" << w << "*x+" << b << endl;
clock_t t2 = clock();
cout << "用时" << t2 - t1 << "毫秒" << endl;
return 0;
}
运行结果如下:
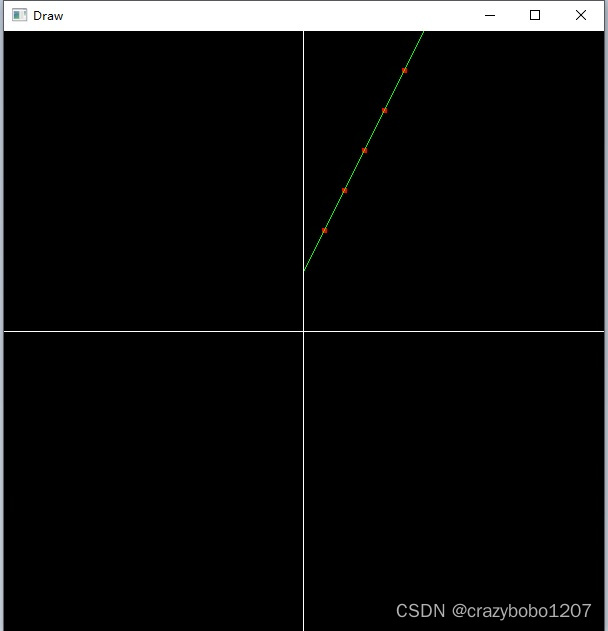
下面验证以上线性回归的结果是否正确(其实可以直接观察到y=2*x+3就是准确解,以上求得的w和b值,与真实值之间的误差是万分之几)。
#include <GL/glut.h>
#include <math.h>
const float ratio = 15.0;
const int pointNum = 5;
const float w = 2.00018;
const float b = 2.99936;
struct Point
{
float x;
float y;
};
Point p[pointNum] = { {1,5},{2,7},{3,9},{4,11},{5,13} };
void draw()
{
glPointSize(1);
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_LINES);
glVertex2f(-1.0, 0);
glVertex2f(1.0, 0);
glEnd();
glBegin(GL_LINES);
glVertex2f(0, -1);
glVertex2f(0, 1.0);
glEnd();
glPointSize(5);
glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_POINTS);
for (int i = 0; i < pointNum; i++)
{
glVertex2f(p[i].x / ratio, p[i].y / ratio);
}
glEnd();
glPointSize(3);
glColor3f(0.0f, 1.0f, 0.0f);
glBegin(GL_LINES);
glVertex2f(0.0 / ratio, (w * 0.0 + b) / ratio);
glVertex2f(10.0 / ratio, (w * 10.0 + b) / ratio);
glEnd();
glFlush();
}
void myDisplay()
{
glClear(GL_COLOR_BUFFER_BIT);
draw();
}
int main(int argc, char* argv[])
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowPosition(100, 100);
glutInitWindowSize(600, 600);
glutCreateWindow("Draw");
glutDisplayFunc(myDisplay);
glutMainLoop();
return 0;
}
画出5个样本点,以及y=2.00018*x+2.99936的直线方程,直线基本穿过5个样本点。